流体力学分野
超音速で航行するジェット機の周りには衝撃波が形 成されます。衝撃波は非常に薄い層で、そこで大気は圧縮され、運動エネルギーは熱エネルギーに変換されますが、その変化はほとんど不連続的です。また機体の表面近くでは境界層の剥離や乱流への遷移等の様々な不安定現象が生じ、流れは非常に複雑になります。本研究室では高速複雑流体の簡便で信頼性の高い数値解法の開発を行い、その過程で生まれた計算法を航空宇宙流体解析に応用する研究を行っています。
当研究室のもう一つの研究テーマは、希薄気流や マイクロ・ナノオーダーの気流の実験的研究で す。このような気体では分子運動論的効果が顕著になり、例えば止まっている壁でも流れが生じたりします。現在、分子運動論的効果を利用した混 合気体の成分分離などを行う様々な新規デバイスの開発に取り組んでいます。

教員
大和田 拓 ( Taku OHWADA )
教授(工学研究科)
研究テーマ
ボルツマン方程式の解析的・数値解析的研究
最近の研究テーマは流体力学方程式の気体論的解法の理論およびこれによる数値解析である。
連絡先
〒615-8540 京都市西京区京都大学桂
(桂キャンパス Cクラスター) C3棟 c3S11室
TEL: 075-383-3771
E-mail: ohwada@kuaero.kyoto-u.ac.jp
担当科目
| 学部 | 大学院 |
|---|---|
|
自然現象と数学(1年前期) 流体力学 (2年後期・3年前期) |
航空宇宙流体力学 (前期) |
杉元 宏 ( Hiroshi SUGIMOTO )
 講師(工学研究科)
講師(工学研究科)
研究テーマ
低圧あるいはミクロな系における気体の振舞いを、希薄気体力学(分子気体力学)に基づく解析・数値解析および実験によって研究しています。
- 希薄気体特有の流れの解明と応用
- 運動する部品が不要の気体ポンプ
- 混合気体分離法の開発
連絡先
〒615-8540 京都市西京区京都大学桂
(桂キャンパス Cクラスター) C3棟 c3S12室
TEL: 075-383-3772
E-mail: sugimoto@kuaero.kyoto-u.ac.jp
担当科目
| 学部 | 大学院 |
|---|---|
|
流体力学 (2年後期・3年前期) 物理数学演習(4年前期) |
航空宇宙流体力学 (前期) |
研究テーマ紹介
気体論スキームの開発とその応用
圧縮性ナビエ・ストークス方程式に対する高精度気体論スキームを開発している。セル境界での数値流束の不連続の取り扱いを工夫することにより、衝撃波問題ならびに境界層問題のどちらにも少ない格子点で良い結果を与える新しい気体論スキームを構成することができる。現在,本スキームを前面ステップまわりの超音速流の計算など、より実際的な問題に適用している。
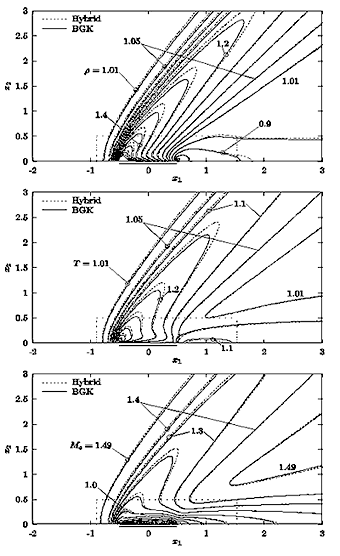
図-1 ハイブリッド法への適用例。平板を過ぎる希薄気流。平板近傍ではBGK方程式に基づく差分法、その外部領域はNS方程式に対する気体論スキームを用いて数値解析した例。全領域をBGK方程式で解析した結果と比較してある。
逆方向ジェットを利用した極超音速空力加熱に対する熱防御
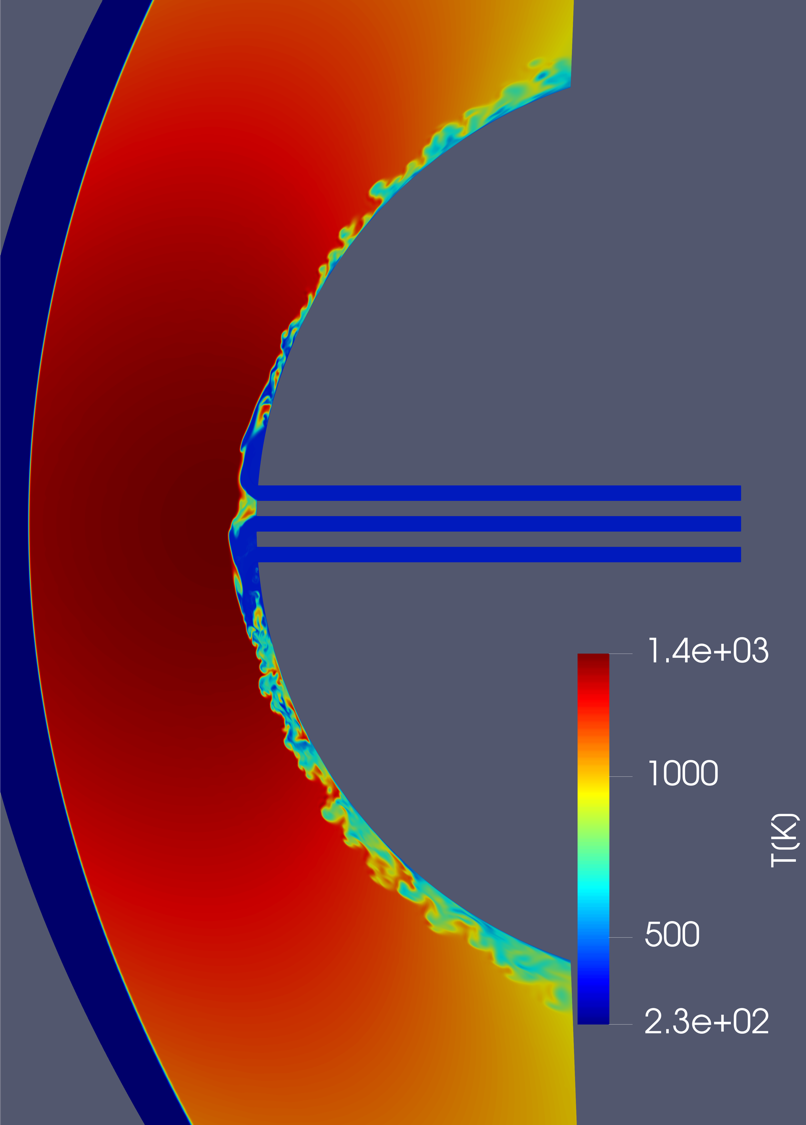
極超音速宇宙機ノーズのアクティブな冷却法として、亜音速 逆方向ジェットによるフィルム冷却の研究を行なっています。2次元の解析では翼前縁付近の熱流は90パーセント近く減少しましたが、3次元解析では種々の不安定現象、乱流遷移により50〜60パーセントにまで低下します。少量の冷媒で高い冷却を行える可能性を探っています。
ボルツマン方程式の高次精度時間積分(DSMC法への適用)
低圧気体あるいは小さな系の気体の振る舞いの数値解析法の一つにDSMC法がある。本研究では、従来のDSMC法の時間精度を考察することにより、時間精度がより優れた新しいDSMC法を提案した。

図-2 時間ステップに対する収束性(1次収束が2次収束に改善されている)
| 従来のDSMC | 粒子の移動(Δt)+粒子衝突(Δt) |
|---|---|
| 新しいDSMC(Strang) | 粒子の移動(Δt/2)+粒子衝突(Δt)+粒子の移動(Δt/2) |
(Δt:時間ステップ)
分子気体効果を利用したポンプ・気体分離法の開発
気体にはたくさんの分子があり,気体全体として静止していた場合でも,それぞれの分子は毎秒数百mの速さで運動しています.その運動をわずかでも取り出せれば,かなりの速さです.普通は分子がすぐに他の分子と衝突するので難しいのですが,高層大気や真空機器内など,分子が少ない場合には,物体の配置や温度を工夫すれば,気体全体の流れとして取り出すことができます.例えば19世紀後半にレイノルズ・マクスウェルが見いだした熱遷移(Thermal Transpiration)では,壁面にそって温度が変化していると,低温側から高温側に気体の流れが生じます.この種の熱駆動流の速さは分子の種類で異なったものになるため,混合気体を窒素や二酸化炭素などの成分に分離することも可能です.

熱遷移流を用いたポンプの概念図

実験装置(2000年)
上図の高温部分と低温部分を切断することにより, 止まった物体で1m/sec以上の流速を出すこともできます.
実験装置(2007年)
この理屈は,例えば紙の繊維の間のミクロな空間でも成り立ちます.現在,数値解析をもとに紙等の多孔膜周囲の温度や圧力を調整し,数十度の温度差だけで大気圧混合気体を分離し続ける装置の開発を進めています.

温度ー濃度変換実験機(2014年)
現在は,一般に通販で入手できる濾紙を用い,任意の混合気体・同位体を分離する実験に取り組んでいます.お湯と水の温度差だけをエネルギー源として,どんな同位体でも分離する装置が目標です.
温度ー濃度変換の原理計算(2012年)
温度ー濃度変換の実証装置(2019年)
